Welcome to the measurement worksheets page at Math-Drills.com where you can measure up, measure down or measure all around! This page includes Measurement worksheets for length, area, angles, volume, capacity, mass, time and temperature in Metric, U.S. and Imperial units.
Measurement concepts and skills give students the ability to perform tasks related to everyday life. Length, area, volume, capacity, mass, time and temperature are measurement concepts that people are exposed to everyday. Students begin using non-standard units such as their own height and progress to using standard measurement units. Being able to recognize and use for comparison, common measurement units such as the metre or foot, allows students to use their estimation skills to help them solve problems in measurement. Measurement tools enable students to learn hands-on and develop a deeper understanding of measurement concepts.
Most Popular Measurement Worksheets this Week



Reading and Converting Temperature Worksheets

Reading temperatures from a thermometer is one of those everyday skills that is transferable to other situations. Sure, students could just ask their smart device about the temperature, but that only tells them the temperature at the nearest weather station, not where they're standing. Wouldn't it be more exciting to look at a thermometer in their own yard? And what if they are working at a solar power farm (or elsewhere) in the future and have other meters and gauges to read? Their skill in reading thermometers will help introduce them to negative numbers and be useful for reading other types of meters and gauges in the future.
Reading Temperatures From Thermometers
Millions of people live near the U.S./Canada border, so it is inevitable that once in a while, those people are going to hear or see the temperature in a less familiar unit. Perhaps traveling to another country has one baffled about the forecast. Having a knowledge of some simple equivalents (like the freezing point is 0 degrees Celsius and 32 degrees Fahrenheit) and the ability to convert between C and F will not only help in determining the temperature in a familiar form, but will also help students build math skills that are useful in other situations. The temperature conversion guide gives a summary of the formulas used and some whole number equivalents to learn. There are several practice sheets for converting from °C to °F, from °F to °C, and a couple with both conversions mixed up.
Temperature Conversion Guide
Measuring and Converting Within Measurement Systems
Measuring length is so much more interesting if you can send students out with rulers and have them measure items in their environment. What is the width of the textbook? the classroom? the school? Have you ever met a student who didn't enjoy using a measuring wheel (you know the one that clicks every time you've traveled a yard or a meter)? How do you know they've measured things correctly though? Well, you might need something like we've provided below. You can also compare students' measurements of the same objects to see if they got the same measurement. Let's say, you had 20 students measure the height of the doorway. You should get 20 very similar answers (unless they are the sharing type then you'll get exactly the same answers) and any different answers can be quickly identified. IMPORTANT: When printing, select "Actual Size" or your measurements may be off.
Measuring Lengths of Bars in Centimeters and Millimeters
Measuring Lengths of Bars in Inches
Just like regrouping when adding, sometimes it is useful to regroup when measuring. If you have too many feet, it might be easier to express your number in yards or miles, for example.
Converting Between U.S. Length Measurements Worksheets
Which unit to use with mass depends a lot on the quantity and what you want to communicate. Whatever your reason for converting mass measurements, these worksheets are likely able to help you take a weight off your shoulders.
Converting Between U.S. Mass Measurements Worksheets
The liquid measurement worksheets include gills because this is the key unit that results in more fluid ounces in an Imperial gallon than in a U.S. gallon. You can learn more about gills in our liquid measurement conversion guide.
U.S. Liquid Measurements Conversion Guide
Converting Between U.S. Liquid Measurements
Even though Imperial and U.S. Customary units may sound the same, they aren't always the same amount. For example, there are 3.785 litres in a U.S. gallon and 4.546 litres in an Imperial gallon. Sometimes there are also different definitions for units like the gill used in liquid measurements. In the U.S., there are 4 fluid ounces in a gill and in the Imperial System, there are 5 fluid ounces in a gill.
Imperial (U.K.) Liquid Measurements Conversion Guide
Converting Between Imperial (U.K.) Liquid Measurements
Converting between Metric units is really an exercise in multiplying and dividing by powers of ten. Each of the converting worksheets in this section includes a "Conversion Line" that includes the prefixes, symbols and powers. It can be used to figure out how many "steps" are required to convert from one unit to another and what operation must be used. For example, when converting from millimeters to kilometers, students would determine that it takes six steps to the left in the direction of the division sign to get from milli to kilo on the conversion line. Depending on which method they are taught, this could involve dividing by 10 six times, dividing by 106 or "moving the decimal" six places to the left. For squared units, each step counts as 100 or 102 and for cubic units, each step counts as 1000 or 103. For more details, please see the Metric system conversion guide.
Converting Within the Metric System Resources
Converting Between Metric Length Measurements Worksheets
Converting Between Metric Mass Measurements Worksheets
Converting Between Metric Volume Measurements Worksheets
Converting Between Common Metric Measurements (Mixed)
Converting Between Metric Area Measurements Worksheets
The Metric or SI system uses thin spaces for thousands separators and spells metres and litres with -re rather than -er. This section is mainly for students in English Canada, however, anyone who uses spaces for thousands separators might like these worksheets. This section is very similar to the previous section except for the differences in number formats and spelling.
Metric System Conversion Guide (SI Format: Spelling and Space-Separated Thousands)
Converting Between Metric Length Measurements Worksheets (SI Format: Space-Separated Thousands)
Converting Between Metric Mass Measurements Worksheets (SI Format: Space-Separated Thousands)
Converting Between Metric Volume Measurements Worksheets (SI Format: Space-Separated Thousands)
Converting Between Common Metric Measurements (Mixed) Worksheets (SI Format: Space-Separated Thousands)
Converting Between Metric Area Measurements Worksheets (SI Format: Space-Separated Thousands)
Similar to the previous two sections; however, these worksheets use dots for thousands separators and commas for decimals. This is often found in languages other than English. Metres and litres are spelled with -re as you would find in many countries outside of the U.S.
Metric System Conversion Guide (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Metric Length Measurements Worksheets (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Metric Mass Measurements Worksheets (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Metric Volume Measurements Worksheets (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Common Metric Measurements (Mixed) Worksheets (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Metric Area Measurements Worksheets (European Format: Period-Separated Thousands and Comma Decimals)
Converting Between Measurement Systems Worksheets

Converting between Metric and U.S. customary units can be accomplished in a number of ways and usually takes a little knowledge of fractions and/or decimals. Most commonly, students will use a formula to convert and round the values. You may like our converting inches and centimeters with rulers worksheets for students who have difficulty with manipulating the numbers and formulas and need an easier method.
Converting Between Inches and Centimeters
Converting Between Inches and Centimeters With a Ruler
Converting Between U.S. and Metric Length Units
Converting Between U.S. and Metric Mass Units
Converting Between U.S. and Metric Volume Units
Converting Between Imperial (U.K.) and Metric Mass Units
Converting Between Imperial (U.K.) and Metric Volume Units
Converting Worksheets For U.S. Nurses
Measuring Angles, Rectangles and Triangles
If they are available, full round protractors help students to recognize that measuring angles is the same as measuring sections of a circle. They also makes it much easier and precise to measure reflex angles.
Measuring Angles
Rectangles are fairly straight-forward polygons to measure since it is easy to find rectangles that use whole numbers. Rectangles are generally used when students first learn about perimeter and area and it is an opportune time to teach students that units are an essential part of any measurement. Without units, numbers are meaningless. Get your students into the habit of expressing all of their measurements with the correct units before they learn how to measure other polygons. Especially make sure they know that area is always expressed with squared units.
If a student is just starting to learn about perimeter and area, a few hands-on activities to learn the concepts is a good idea. Have them use square tiles to cover an area, have them paint a piece of paper and see how much paint is required. Create rectangles with straws and pipe cleaners and fill with square tiles to differentiate between perimeter and area. See if there are differently shaped rectangles that will hold the same number of square tiles.
Perimeter and Area of Rectangles Worksheets
Perimeter and Area of Rectangles Worksheets (Retro)
Calculating Other Rectangle Measurements Using Perimeter and Area
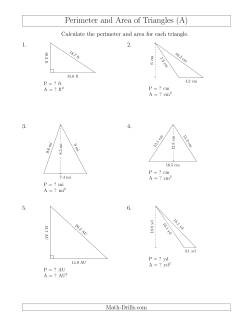
If you want students to understand the triangle area formula, you might want to study parallelograms and rectangles first. Once students get how area is calculated for rectangles and parallelograms, they simply need to cut parallelograms and rectangles in half diagonally to get related triangles. They should quickly see that the area of a triangle is simply half of the area of the related quadrilateral.
Area and Perimeter of Triangles Worksheets
Area and Perimeter of Triangles Worksheets (Retro)
Calculating Other Triangle Measurements (Angles, Heights, Bases)
Measuring Other Polygons

Area and Perimeter of Parallelograms Worksheets
Area and Perimeter of Trapezoids Worksheets
Calculating Other Trapezoid Measurements Worksheets
Area and Perimeter of Trapeziums Worksheets (U.K. Format: Name of Shape)
Calculating Other Trapezium Measurements Worksheets (U.K. Format: Name of Shape)
The shapes are mixed up on the worksheets in this section. These area and perimeter worksheets would be best suited to students who have mastered finding the areas of triangles, rectangles, parallelograms, and trapezoids.
Calculating the Area and Perimeter of Various Shapes
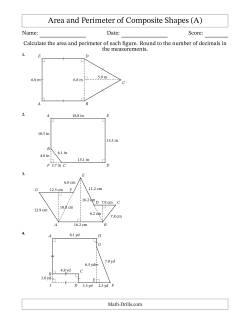
Compound or composite shapes are polygons that are made up of simpler shapes such as triangles and rectangles. Calculating the area of composite shapes involves calculating the areas of the simpler shapes. Calculating the perimeter involves determining which sides are on the outside of the composite shape and adding up their lengths. Sometimes this requires further calculations of hypotenuses and arc lengths or deriving side measurements from other measurements. For the more technical, assume that any horizontal or vertical measurement is precise and other measurements are derived and often rounded. This affects the number of significant digits, of course, but these worksheets take a simpler approach and ask students to round their answers to the number of decimal places used in the measurements.
Calculating the Area and Perimeter of Compound/Composite Shapes
Measuring Circles

Radius, diameter, circumference and area are all related measurements; you only need one of them to find the remaining measurements. Diameter and radius are the simplest ones because the diameter of a circle is twice the radius and, conversely, the radius is half the diameter. To calculate between radius/diameter and circumference/area, you need to use π (pi). Depending on your accessibility to calculators or computers, you may use many digits of pi in the calculation or just a few. Often, people without calculators use an estimate of pi (3 or 3.14). Just for fun we made a worksheet with pi to 100,000 decimal places. The calculations on the worksheets below use a fairly precise version of pi; you may have to adjust the answers if you use more rounded versions of pi.
Pi to 100K Decimal Places Reference
Circle Measurements Worksheets (Area, Circumference, Diameter, Radius)
Calculating Arc Lengths
Calculating Arc Angles
Calculating Arc Lengths and Angles
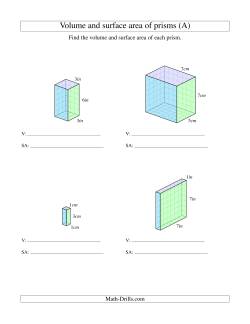
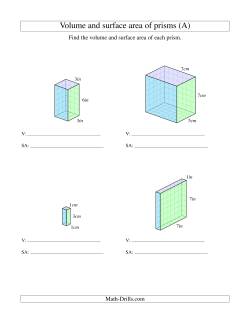
Measuring Three-Dimensional Forms