Welcome to the geometry worksheets page at Math-Drills.com where we believe that there is nothing wrong with being square! This page includes Geometry Worksheets on angles, coordinate geometry, triangles, quadrilaterals, transformations and three-dimensional geometry worksheets.
Get out those rulers, protractors and compasses because we've got some great worksheets for geometry! The quadrilaterals are meant to be cut out, measured, folded, compared, and even written upon. They can be quite useful in teaching all sorts of concepts related to quadrilaterals. Just below them, you'll find worksheets meant for angle geometry. Also see the measurement page for more angle worksheets. The bulk of this page is devoted to transformations. Transformational geometry is one of those topics that can be really interesting for students and we've got enough worksheets for that geometry topic to keep your students busy for hours.
Don't miss the challenging, but interesting world of connecting cubes at the bottom of this page. You might encounter a few future artists when you use these worksheets with students.
Most Popular Geometry Worksheets this Week





Lines and Angles
In this section, there are worksheets for two of the basic concepts of geometry: lines and angles.
Lines (or straight lines to be precise) in geometry are continuous and extend in both directions to infinity. They have no width, depth or curvature. In math activities, they are often represented by a drawn straight path with some width. To show that they are lines, arrows are drawn on each end to show they extend to infinity. A line segment is a finite section of a line. Line segments are often represented with points at each end of a drawn straight path. Rays start at a point and extend in a straight line to infinity. This is shown with a point at one end of a drawn straight path and an arrow at the other end.
Identifying Lines, Line Segments and Rays
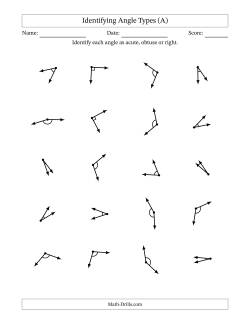
Angles can be classified into six different types. Acute angles are greater than 0 degrees but less than 90 degrees. Right angles are exactly 90 degrees. Obtuse angles are greater than 90 degrees but less than 180 degrees. Straight angles are exactly 180 degrees. Reflex angles are greater than 180 degrees but less than 360 degrees. Complete/Full angles are exactly 360 degrees.
Identifying Angle Types Worksheets
There are several angle relationships of which students should be aware. Complementary angles are two angles that together form a 90 degree angle; supplementary angles are two angles that together form a 180 degree angle; and explementary angles are two angles that together form a 360 degree angle. Vertical angles are found at line intersections; angles opposite each other are equal. Students can practice determining and/or calculating the unknown angle(s) in the following angle relationships worksheets.
Angle Relationships Worksheets
Angles of Transversals Intersecting Parallel Lines
Measuring angles worksheets, can be found on the Measurement Page
Triangles, Quadrilaterals and Other Shapes

The quadrilaterals set can be used for a number of activities that involve classifying and recognizing quadrilaterals or for finding the properties of quadrilaterals (e.g. that the interior angles add up to 360 degrees). The tangram printables are useful in tangram activities. There are several options available for the tangram printables depending on your printer, and each option includes a large version and smaller versions. If you know someone with a suitable saw, you can use the tangram printable as a template on material such as quarter inch plywood; then simply sand and paint the pieces.
Shape Sets
Identifying Regular Polygons
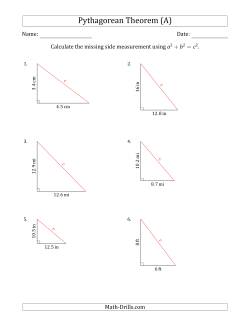
Worksheets for classifying triangles by side and angle properties and for working with Pythagorean theorem.
If you are interested in students measuring angles and sides for themselves, it is best to use the versions with no marks. The marked versions will indicate the right and obtuse angles and the equal sides.
Classifying Triangles Worksheets
A cathetus (plural catheti) refers to a side of a right-angle triangle other than the hypotenuse.
Calculating Triangle Dimensions Using Pythagorean Theorem
Trigonometric ratios are useful in determining the dimensions of right-angled triangles. The three basic ratios are summarized by the acronym SOHCAHTOA. The SOH part refers to the ratio: sin(α) = O/H where α is an angle measurement; O refers the length of the side (O)pposite the angle measurement and H refers to the length of the (H)ypotenuse of the right-angled triangle. The CAH part refers to the ratio: cos(α) = A/H where A refers to the length of the (A)djacent side to the angle. The TOA refers to the ratio: tan(α) = O/A.
Calculating Angles and Sides Using Trigonometric Ratios
Quadrilaterals are interesting shapes to classify. Their classification relies on a few attributes and most quadrilaterals can be classified as more than one shape. A square, for example, is also a parallelogram, rhombus, rectangle and kite. A quick summary of all quadrilaterals is as follows: quadrilaterals have four sides. A square has 90 degree corners and equal length sides. A rectangle has 90 degree corners, but the side lengths don't have to be equal. A rhombus has equal length sides, but the angles don't have to be 90 degrees. A parallelogram has both pairs of opposite sides equal and parallel and both pairs of opposite angles are equal. A trapezoid only needs to have one pair of opposite sides parallel. A kite has two pairs of equal length sides where each pair is joined/adjacent rather than opposite to one other. A bowtie is sometimes included which is a complex quadrilateral with two sides that crossover one another, but they are readily recognizable. Any other four-sided polygon can safely be called a quadrilateral if it doesn't meet any of the criteria for a more specific classification.
Classifying Quadrilaterals
Coordinate Plane Worksheets

Coordinate point geometry worksheets to help students learn about the Cartesian plane.
Plotting Random Coordinate Points
There are many other Cartesian Art plots scattered around the Math-Drills website as many of them are associated with a holiday. To find them quickly, use the search box.
Cartesian Art
Coordinate Plane Distance and Area
Transformations Worksheets
Transformations worksheets for translations, reflections, rotations and dilations practice.
Here are two quick and easy ways to check students' answers on the transformational geometry worksheets below. First, you can line up the student's page and the answer page and hold it up to the light. Moving/sliding the pages slightly will show you if the student's answers are correct. Keep the student's page on top and mark it or give feedback as necessary. The second way is to photocopy the answer page onto an overhead transparency. Overlay the transparency on the student's page and flip it up as necessary to mark or give feedback.
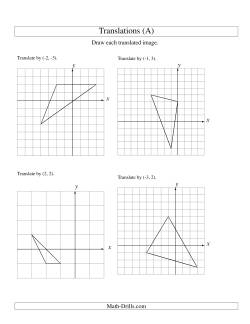
Also known as sliding, translations are a way to mathematically describe how something moves on a Cartesian plane. In translations, every vertex and line segment moves the same, so the resulting shape is congruent to the original.
Translations Worksheets
Translations Worksheets (Multi-Step)
Reflect on this: reflecting shapes over horizontal or vertical lines is actually quite straight-forward, especially if there is a grid involved. Start at one of the original points/vertices and measure the distance to the reflecting line. Note that you should measure perpendicularly or 90 degrees toward the line which is why it is easier with vertical or horizontal reflecting lines than with diagonal lines. Measure out 90 degrees on the other side of the reflecting line, the same distance of course, and make a point to represent the reflected vertex. Once you've done this for all of the vertices, you simply draw in the line segments and your reflected shape will be finished.
Reflecting can also be as simple as paper-folding. Fold the paper on the reflecting line and hold the paper up to the light. On a window is best because you will also have a surface on which to write. Only mark the vertices, don't try to draw the entire shape. Unfold the paper and use a pencil and ruler to draw the line segments between the vertices.
Reflections Worksheets
Reflections Worksheets (Multi-Step)
Here's an idea on how to complete rotations without measuring. It works best on a grid and with 90 or 180 degree rotations. You will need a blank overhead projector sheet or other suitable clear plastic sheet and a pen that will work on the page. Non-permanent pens are best because the plastic sheet can be washed and reused. Place the sheet over top of the coordinate axes with the figure to be rotated. With the pen, make a small cross to show the x and y axes being as precise as possible. Also mark the vertices of the shape to be rotated. Using the plastic sheet, perform the rotation, lining up the cross again with the axes. Choose one vertex and mark it on the paper by holding the plastic sheet in place, but flipping it up enough to get a mark on the paper. Do this for the other vertices, then remove the plastic sheet and join the vertices with line segments using a ruler.
Rotations Worksheets
Rotations Worksheets (Multi-Step)
Dilations Worksheets
Determining Scale Factors Worksheets
Mixed Transformations Worksheets (Multi-Step)
Constructions Worksheets
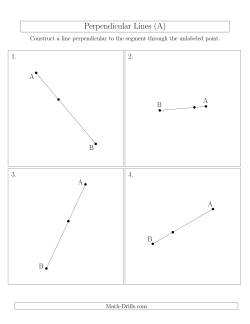
Constructions worksheets for constructing bisectors, perpendicular lines and triangle centers.
It is amazing what one can accomplish with a compass, a straight-edge and a pencil. In this section, students will do math like Euclid did over 2000 years ago. Not only will this be a lesson in history, but students will gain valuable skills that they can use in later math studies.
Constructing Midpoints And Bisectors On Line Segments And Angles
Constructing Perpendicular Lines
Constructing Triangle Centers
Three-Dimensional Geometry
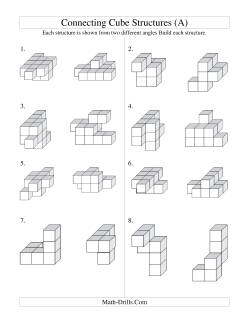
Three-dimensional geometry worksheets that are based on connecting cubes and worksheets for classifying three-dimensional figures.
Connecting cubes can be a powerful tool for developing spatial sense in students. The first two worksheets below are difficult to do even for adults, but with a little practice, students will be creating structures much more complex than the ones below. Use isometric grid paper and square graph paper or dot paper to help students create three-dimensional sketches of connecting cubes and side views of structures.
Connecting Cube Structures
Classifying Three-Dimensional Figures
This section includes a number of nets that students can use to build the associated 3D solids. All of the Platonic solids and many of the Archimedean solids are included. A pair of scissors, a little tape and some dexterity are all that are needed. For something a little more substantial, copy or print the nets onto cardstock first. You may also want to check your print settings to make sure you print in "actual size" rather than fitting to the page, so there is no distortion.
