Welcome to the number sense page at Math-Drills.com where we've got your number! This page includes Number Worksheets such as counting charts, representing, comparing and ordering numbers worksheets, and worksheets on expanded form, written numbers, scientific numbers, Roman numerals, factors, exponents, and binary numbers. There are literally hundreds of worksheets meant to help students develop their understanding of numeration and number sense.
In the first few sections, there are some general use printables that can be used in a variety of situations. Hundred charts, for example, can be used for counting, but they can just as easily be used for learning decimal hundredths. Rounding worksheets help students learn this important skill that is especially useful in estimation.
Comparing and ordering numbers worksheets help students further understand place value and the ordinality of numbers. Continuing down the page are a number of worksheets on number forms: written, expanded, standard, scientific, and Roman numerals. Near the end of the page are a few worksheets for older students on factors, factoring, exponents and roots and binary numbers.
Most Popular Number Sense Worksheets this Week






Reading and Writing Numbers
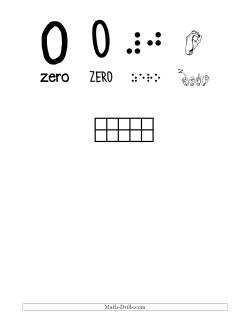
There are a few different number posters in this section. The first two, with bird and butterfly themes include various ways of representing numbers from 0 to 9. Two versions of the numerals are used to demonstrate different printing styles, a Braille version and an American Sign Language version are also included to make students aware of different ways of representing each number. A linear representation and a ten-frame representation follow which is then followed by a pictorial representation using the theme. The poster sized numbers are just that ... made for printing and putting up in your classroom or home school.
Number Recognition Posters
Poster-Sized Numbers
Distinguishing between even and odd numbers is an important skill for young students to learn. The vocabulary of even and odd is used throughout their math education, so it is necessary to learn it as soon as possible. Connecting cubes can help a great deal in visually demonstrating odd and even numbers. Create the numbers from 1 to 10 (or more) using connecting cubes in pairs and students will quickly see that the odd numbers have an unpaired cube that can be thought of as the "odd cube out." Once they have seen this pattern, they may be able to extend the pattern without making cube models. Ask them about 11 and 12 and 35 and so on.
Even and Odd Numbers
In the writing numerals to 20 worksheets, you will find that the A version includes all numbers, B to E versions have about half the numbers included, F to I versions have about a third of the numbers included and the J version includes no numbers... just the lines to write them on. All versions include dashes under the numbers, so students have a reference for where to place the numbers. You can access the other versions (B to J) once you select the A version you want below.
Practice Writing Numerals from 0 to 20
Practice Writing One Numeral at a Time
The main idea of learning to write numbers in words is to be able to say numbers correctly. In the past it might also have been useful for writing checks/cheques, but there isn't a lot of that going on any more. In writing, numbers up to ten are generally written as words and above ten as numerals. Numbers that are at the beginning of sentences are often written as words. These worksheets do not use the superfluous "and" throughout. If this is something you would like included, please send some feedback.
Writing Small Numbers in Words
Writing Large Numbers in Words (Comma-Separated Thousands)
Writing Large Numbers in Words (Space-Separated Thousands)
Now, let's see if students can write the numbers that are written! The reading numbers written as words worksheets do not have format options as the student question sheets are all written in words. The answer keys are formatted with a comma thousands separator when necessary.
Reading Smaller Written Numbers
Counting Worksheets

Ten frames help students visualize numbers in relation to 10. They are used for many purposes, but the worksheets below are introductory and familiarize students with ten frames and give them practice using them.
Identify Ten Frames
Draw Ten Frames
These skip counting worksheets include pictorial representations of the items the student is counting. For example, in the counting by 3's worksheet, students will see groups of three cars. This allows students to develop a mental image of skip counting. With larger numbers, including groups of items become impractical, so numbers are instead printed on the cars.
Skip Counting by Numbers 1 to 10
Skip Counting by Numbers Greater Than 10
Hundred charts are useful not only for learning counting but for many other purposes in math. For example, a hundred chart can be used to model fractions and to convert fractions into decimals. Modeling 1/4 on a hundred chart would require coloring every fourth square. After coloring every fourth square, there would be 25 squares colored in which is 25/100 or 0.25. Not magic, just math. Hundred charts can also be used as graph paper for graphing, learning long multiplication and division or any other purpose. A common use for hundred charts in older grades is to use it to find prime and composite numbers using the sieve of Eratosthenes.
Filled and Blank 100 Charts
Partially Filled 100 Charts
Have you ever thought about why hundred charts start at the top and count left to right and top to bottom? After all, don't we count UP rather than down? Thermometers have smaller numbers at the bottom, elevation increases the further you go up, and liquids fill from the bottom up. Coordinate grids have decreasing numbers going down and increasing numbers going up. Maybe starting with one at the bottom makes a lot more sense to students than starting with one at the top.
Filled and Blank Bottom-Up 100 Charts
Partially Filled Bottom-Up 100 Charts
120 charts are very similar to hundred charts except they include the numbers from 101 to 120. 120 is a nice number for many reasons. One reason is that it has a lot of divisors—16 in fact. This makes the number 120 useful for many different grouping activities. Another reason is the Common Core Curriculum in the United States requires first graders to count to 120. A third reason is that 120 includes some three-digit numbers which could be a good introduction for some students into the hundreds place.
Filled and Blank 120 Charts
Partially Filled 120 Charts
Similar to the bottom-up 100 charts, the bottom-up 120 charts start counting at the bottom and increase as you go up. Still not convinced that these make sense? Here are some more examples of things that start counting at the bottom: your height, snow depth, floors in a building, scales on most graphs, and altitude.
Filled and Blank Bottom-Up 120 Charts
Partially Filled Bottom-Up 120 Charts
Ninety-nine charts include zero and have no three-digit numbers. Each row starts with a multiple of ten rather than ending with a multiple of ten.
Filled and Blank 99 Charts
Partially Filled 99 Charts
You may not realize that many things start counting at zero, like when you are running around a track; you start at zero laps and count one for every lap you do. These charts start at zero at the bottom and go up to 99 at the top.
Filled and Blank Bottom-Up 99 Charts
Partially Filled Bottom-Up 99 Charts
Counting collections of things in various patterns helps students develop shortcuts and strategies for counting. For example, when students count collections of items in rectangular patterns, they may use skip counting or multiplying to speed up their counting.
Counting Animals Arranged in Patterns
Counting and skip counting can be accomplished with number lines.
Counting and Skip Counting on Number Lines
A skill that is useful is to be able to continue counting or skip counting from any number.
Continue Counting and Skip Counting From Various Numbers
Similar to the counting from any number worksheets, this one asks students to count down from different numbers.
Continue Counting Backwards
Rounding Numbers Worksheets
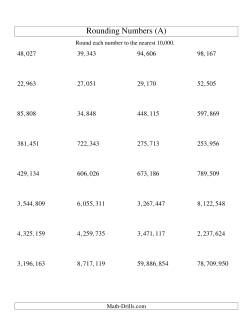
Not only does rounding further an understanding of numbers, it can also be quite useful in estimating and measuring. There are many every day situations where a precise number isn't needed. For example if you needed to paint your basement floor, you don't really need to find out the area to exact square inch since you don't buy paint that way. You get a good idea of the floor space (e.g. it is roughly 20 feet by 15 feet) then read the label on the can to see how many square feet the can of paint covers (which, by the way is also a rounded number and variable depending on the roller used, the porosity of the floor, etc.) and buy enough cans to cover your floor.
Rounding Numbers
Canadian (SI) Format Rounding Numbers
European Format Rounding Numbers
Comparing and Ordering/Sorting Numbers
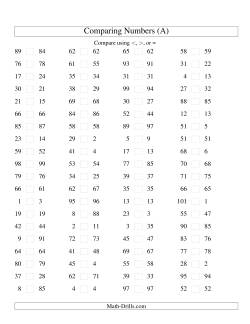
There are many situations where it is important to know the relative size of one number to another. Several words are used to describe the relative sizes of one number to another, but it is probably best to use lesser than, greater than and equal to, although other words are more appropriate in certain situations. For example, if you were comparing two groups of candies, you would probably say, "there are fewer candies in that pile than in that one." The use of the word, "tight", in the worksheet titles means the numbers to be compared are close to one another.
Comparing Small Numbers
Comparing Large Numbers
Canadian (SI) Format Comparing Large Numbers
European Format Comparing Large Numbers
Converting Numbers to Different Forms

When writing numbers in expanded form, students might use one of three forms which will be demonstrated using the number 9753. The first form is quite simple and combines both the place and the place value. For example, 9 is in the thousands place which means the value of that 9 is 9000. The 7 is in the hundreds place which makes it 700. The 5 is in the tens place which makes it 50 and the 3 is in the ones place which makes it 3.
To write in "simple" expanded form, simply separate these four values with plus signs: 9000 + 700 + 50 + 3.
In expanded factors form, the place and the place value are separated with multiplication signs: (9 × 1000) + (7 × 100) + (5 × 10) + (3 × 1). Parentheses are included for clarity.
In expanded exponential form, the place values are expressed as powers of ten: (9 × 103) + (7 × 102) + (5 × 101) + (3 × 100).
Converting Standard Form Numbers to Expanded Form
Converting Standard Form Numbers to Expanded Factors Form
Converting Standard Form Numbers to Expanded Exponential Form
Converting Expanded Form Numbers to Standard Form
Converting Expanded Factors Form Numbers to Standard Form
Converting Expanded Exponential Form Numbers to Standard Form
These versions use a space as a thousands separator.
Canadian (SI) Format Converting Standard Form Numbers to Expanded Form
These versions use a period as a thousands separator.
European Format Converting Standard Form Numbers to Expanded Form
The standard, expanded and written forms conversion worksheets include three number forms on the same page.
Converting Between Standard, Expanded and Written Form Numbers
Canadian (SI) Format Converting Between Standard, Expanded and Written Form Numbers
Convert Numbers in Standard Form to Scientific Notation
Convert Numbers in Scientific Notation to Standard Form
Convert Numbers Between Standard Form and Scientific Notation
This is about as "old school" as you can get. Put on your tunic and pick up your scutum to tackle the worksheets on Roman Numerals. Below, you will see options for standard and compact forms. The standard form Roman Numeral math worksheets include numerals in the commonly-taught version where 999 is CMXCIX (i.e. write the numeral one place value at a time). The compact versions are for those who want more of a challenge where the Roman numerals are written in as concise a version as possible. In the compact version, 999 is written as IM (i.e. one less than 1000).
Converting Roman Numerals to Standard Form Numbers
Converting Compact Roman Numerals to Standard Form Numbers
Operations with Roman numerals

Adding Roman Numerals
Subtracting Roman Numerals
Multiplying Roman Numerals
Dividing Roman Numerals
Mixed Operations With Roman Numerals
Factors and Factoring

What would factoring be without some factoring trees? They are probably the most elegant and convenient way to find the prime factors of a number, but they take a little practice, which is where we come in. The worksheets below are of two types. The first is finding all of the factors of a number. This is great for students who know their multiplication/division facts. If they don't, they might find this a little frustrating, so go back and work on that first. The second type is finding prime factors which we've chosen to do with tree diagrams. Among other things, this is a great way to find prime numbers and to practice divisibility rules.
Lists of Factors
Determining Factors of Numbers
Lists of Prime Factors
Determining Prime Factors Using a Tree Diagram
Calculating Greatest Common Factor Using Prime Factors
Determining Greatest Common Factor Using All Factors
Least Common Multiple (LCM) Worksheets

Determine Least Common Multiple from Multiples
Determine Least Common Multiple from Prime Factors
Exponents and Roots

Squares of Numbers
Square Roots
Squares and Square Roots Mixed
Cubes of Numbers
Cube Roots
Cubes and Cube Roots
Exponents in Factor Form
Other Base Number Systems
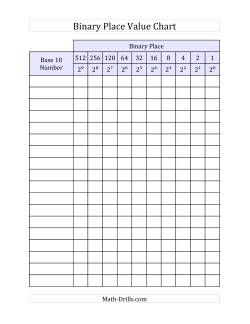
The binary number system has broad applications, but it is most known for its predominance in computer architecture. Learning about the binary system not only encourages higher order thinking, but it also prepares students for further studies in mathematics and computer studies. The chart below may be useful for students who need some help lining things up and learning about place value as it relates to the binary system. We included a base 10 number column, so you can use the chart for converting between decimal and binary systems.
Binary Place Value Chart
The mystery number trick below is actually based on binary numbers. As you may know, each place in the binary system is a power of 2 (1, 2, 4, 8, 16, etc.). Since every decimal (base 10) number can be expressed as a binary number, each decimal number can therefore be expressed as a sum of a unique set of powers of 2. It is this concept that makes this trick work. You might notice that the largest decimal number on the cards is 63 which is also the largest 6-digit binary number (111111). The target position on each version of the mystery number trick contains the powers of 2 associated with the first 6 place values in the binary system (1, 2, 4, 8, 16, 32). Each of the 6 cards represents a specific place value. All 32 numbers on each card contain a 1 in the associated place when written in binary. Basically, when the "friend" identifies the cards that contain the mystery number, they are giving you a binary number that simply needs converting into a decimal number. Just for fun, we mixed up the numbers on the cards and the target position on versions C to J. Version A includes numbers in ascending order and version B includes numbers in descending order. The other versions (B to J) will be available once you click on the A version below.
Binary Mystery Number Trick
Converting from Decimal Numbers to Other Base Number Systems
Converting from Binary Numbers to Other Base Number Systems
Converting from Octal Numbers to Other Base Number Systems
Converting from Hexadecimal Numbers to Other Base Number Systems
Converting from Various Base Numbers to Other Base Number Systems
Help with Converting Between Base Number Systems:
There are shortcuts for converting between some bases. For example, converting from binary to octal takes little effort since 8 is a power of 2. Each group of 3 digits in a binary number represents a single digit in an octal number. For example, 1112 (the 2 stands for binary or base 2) is 78 (the 8 stands for octal or base 8). The simple way to convert binary numbers to octal numbers is to group the binary number into groups of three digits. For example, 1110101010001112 could be written as 111 010 101 000 111. Converting each group into octal means multiplying the first digit of each group by 4, the second digit by 2 and the third digit by 1 then adding the results together. This will result in digits no larger than 7 (since 4 + 2 + 1 = 7) and the number will be converted to base 8. In octal, therefore, the number is 725078. If you can express the octal numbers from 0 to 7 in binary, you can easily convert the other way. For example 72238 = 1110100100112 since 7 is 111, 2 is 010, and 3 is 011 in binary.
A similar shortcut for converting between binary and base 4 numbers involves looking at binary numbers in groups of 2. Similarly, converting from base 3 to base 9 and base 4 to base 16 involves groups of two. Converting from binary to hexadecimal would involve groups of 4.
For other conversions, a commonly used tactic is to convert to decimal as an intermediate step since this is the base system that is probably ingrained in your brain, so it is much more intuitive. For example, converting from a base 5 number to a base 7 number would involve first converting the base 5 number to base 10. To convert, it is only necessary to know the place values of the system that you are converting from and to. In base 5, the lowest place value (furthest to the right) of whole numbers is 1 followed by 5, 25, 125 and so on. In base 7, the place values are 1, 7, 49, 343 and so on. First multiply the digits in the base 5 number by its place values, then divide the resulting decimal number by the base 7 place values and you will have your conversion. For example 43315 is expanded to (4 × 125) + (3 × 25) + (3 × 5) + (1 × 1) = 500 + 75 + 15 + 1 = 591 (in base 10). To continue into base 7, there are at least two ways, the second method is in the next paragraph. For simplicity's sake, take the largest base 7 place value that will divide into 591 at least once. In this case it is 343 which goes into 591 exactly once (1) with a remainder of 248. Divide the remainder by the next place value down, 49, to get (5) with a remainder of 3. Divide 3 by 7 which is (0) with a remainder of 3. Finally, divide by 1 which should leave no remainder, and it is (3) in this case. Put all those digits together and you should have your number in base 7: 15037.
A method to convert directly from one base system to another involves knowing how to divide in the base system you want to convert from. It is fairly easy if you are familiar with the base system. Simply divide the number by the base you want to convert to (but express it in the original base system). Repeat until the division results in 0 with or without a remainder. Convert the remainders and put them in reverse order for the number in the new base system. For example, convert 37508 to hexadecimal (base 16). 16 in base 8 is 208. The first step is to divide 37508 by 208 = 1768 R 108. Next, divide 1768 by 208 to get 78 R 168. Finally, 78 divided by 208 is 08 R 78. Convert the remainders to base 16 (which you may have to think of in terms of decimal numbers, or you can use your fingers and some toes) and write the digits in reverse order. 78 is 716, 168 is (14 in decimal) E16, and 108 is 816. So, the number 37508 is 7A816.
